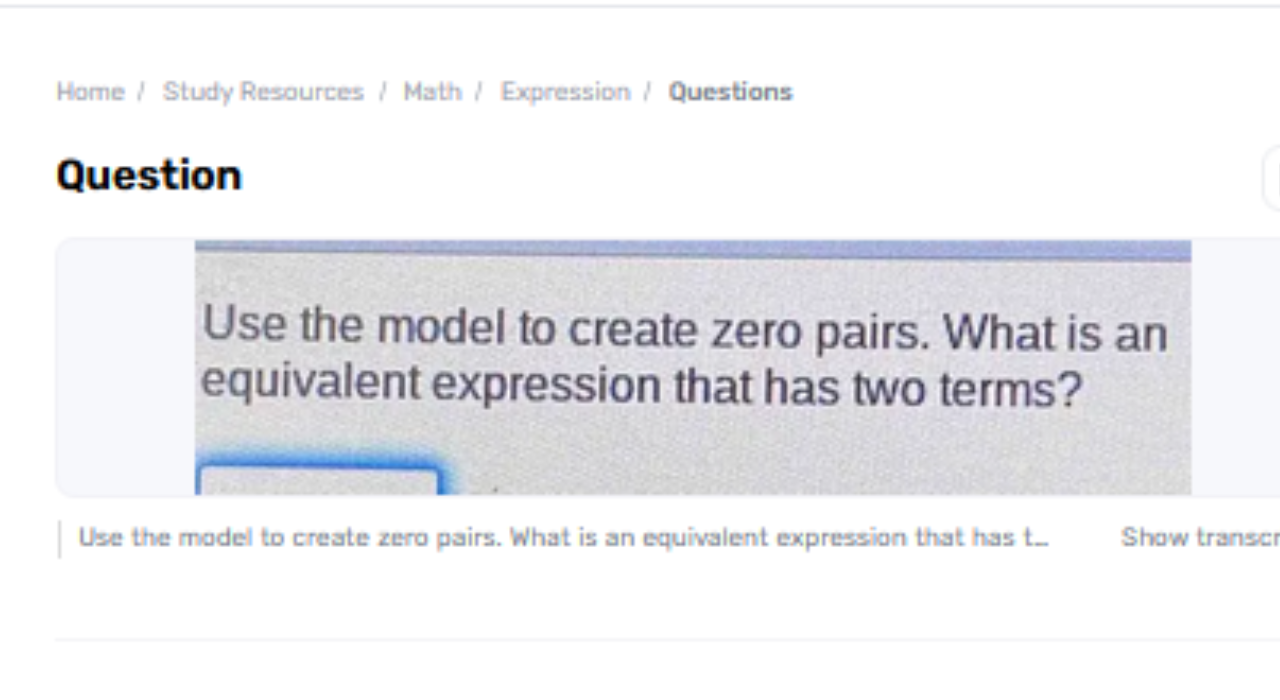
In algebra, creating zero sets could be a method utilized to rearrange expressions and illuminate conditions. A zero match comprises two numbers or terms that cancel each other out, such as +1 and -1 This concept is essential in understanding how to control and disentangle arithmetical expressions. By utilizing zero sets, one can change a complex expression into an identical, less complex shape with fewer terms. This talk will clarify the concept use the model to create zero pairs. what is an equivalent expression that has two terms? of zero pairs, and how to utilize them to streamline expressions, and will illustrate the method through a case that diminishes an expression to two terms.
Understanding Zero Sets
Zero sets are sets of terms that include up to zero. In var variable-based, they are frequently utilized to rearrange expressions by canceling out terms. For occurrence, +3 and -3 shashapeszero combine since their whole is zero: +3+(-3)=0. Additionally, xxx and -x too shape a zero combined. The rule behind zero sets is that including or subtracting zero does not alter the esteem of an expression. This property permits us to present or remove zero sets in expressions to disentangle them.
Making Zero Sets in Arithmetical Expressions
To form zero sets in a logarithmic expression, distinguish sets of terms that cancel each other out. Consider the expression 4x-3+2x+3-2x. Able to modify and gather terms to distinguish zero sets: 4x, In this expression, 2x and -2x- shape a zero combine, and -3 and +3 shape another zero combine. By canceling these sets, the expression rearranges to: 4x
This preparation shows how zero sets can be utilized to decrease an expression to a simpler shape.
Disentangling an Expression to Two Terms
Let’s apply the concept of zero sets to disentangle an expression to two terms. Consider the expression 3a+5b-a-2b+2a We can utilize zero sets to disentangle it: First, gather the like terms: (3a-a+2a)+(5ba2b) Following, streamline each gathers: (3a-a+2a)=4a (5b-2b)=3b (5b – 2b) = 3b(5b-2b)=3b In this way, the disentangled expression is: 4a+3b In this case, the terms aaa and (part of the initial gathering) canceled out to make zero pairs, allowing us to decrease the expression to fair two terms: 4a and 3b.
Identical Expression with Two Terms
Utilizing the strategy of making zero sets, we have changed the first expression 3a+5ba-2b+5 into the comparable expression 4a+3b. This proportionate expression holds the same esteem as the initial but is streamlined to contain as it were two terms. The method of rearranging expressions through zero sets could be an effective device in variable-based math that can make tackling conditions and performing calculations much more reasonable.
Steps to Address a Gauth Inquiry
1. Interpret the Address:
Recognize if the inquiry is around the setup, utilization, administration, or investigation of Gauth. This guarantees a centered reaction.
2. Collect Data:
Counsel Gauth’s official guides and bolster materials. Considercommonplace issues clients face to give a exhaustive reply.
3. Draft the Reaction:
Structure the reply in clear, coherent steps or areas. Ensure each point is brief and straightforwardly important to the address.
4. Review and Alter:
Confirm the precision of the data. Alter the reaction for clarity and brevity, guaranteeing it is simple to get and free from pointless points of interest.
Conclusion
Making zero sets may be a valuable procedure in polynomial math for rearranging expressions and understanding conditions. By recognizing and canceling out sets of terms that entirety to zero, complex expressions can be reduced to easier, more reasonable shapes. In the case talked about, the expression 3a+5b-2b+2a was streamlined to 4a+3b through the utilization of zero sets. Understanding and applying this method makes a difference in streamlining logarithmic operations and gives a clearer way to find arrangements. Acing the utilization of zero sets is basic for understudies and experts working with logarithmic expressions.